ANSWERS
1) Equator is extended for 360 degrees;2) The other Arcs of Latitudes, Northern and Southern of the Equator Arc, measure all 360 degrees.
3) They all correspond to a one full arc of Latitude.
4) 6,935 Miles between WASHINGTON DC and KABUL
5) Areas and Countries located closer to Equator have normal size, those closer to Poles are bigger.
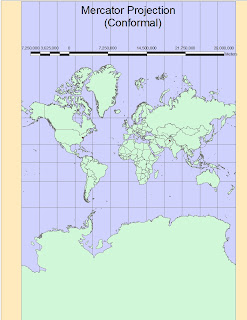
6) 6,865 Miles with the Mercator projection (CONFORMAL-1)
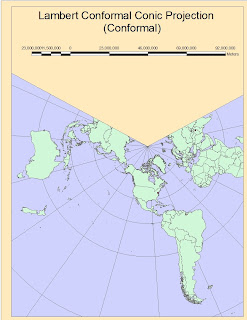
7) 6,800 Miles with the Lambert Conformal Conic (CONFORMAL-2)
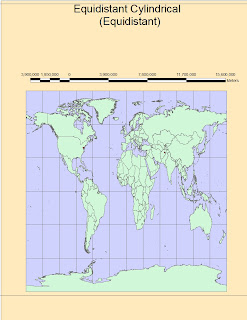8) 5,065 Miles with the Equidistant Cylindrical (Equidistant-1)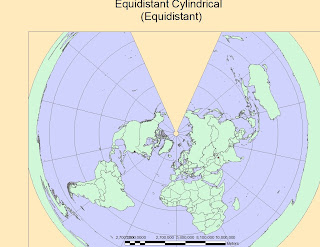
9) 6,970 Miles with Equidistant Conic (Equidistant-2)
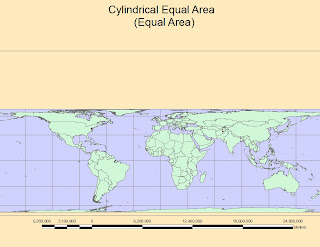10) 10,190 Miles with Cylindrical Equal Area (Equal Area-1)
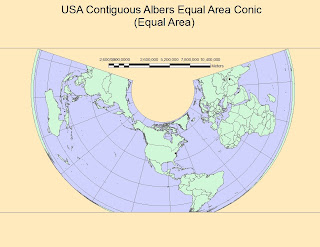11) 7,270 Miles with USA Contiguous Albers Equal Area Conic (Equal Area-2)THE IMPORTANCE OF DIFFERENT PROJECTIONS IN CREATING MAPS AND GEOGRAPHY
the significance, perils and potential of map
projections based on this exercise. Be sure to clearly reference your six maps as
examples
Geographical Projections are used to reduce surfaces of spherical or other 3D shapes into a 2D models. Inevitably, some information is lost during this process, as it is not possible to represent a Sphere on a Plane. One important characteristic or projection process is that it can be adapted to different needs. In fact, there are basically infinite formulas we can use for making surfaces from Geometrical Shapes. It depends by the Intersecting point we use as a touching point from the hypothetical surface and the sphere (or ellipsoid), and which surface are we going to use to represent the plane. We can use for example a plane developed from a Cone or a Cylinder, or other shape with a curvature.
Personally, I think that one of the best projection is the Mercator secant in two points of the globe, because is able to also maintain areas better than a normal Mercator. This Projection uses a normal cylinder, but it has tangent 2 points at 30 degrees North and 30 Degrees South of the Equator with the Sphere. Areas North of 30 deg. North and South of 30 deg. South will be slightly bigger than the reality, while the arc between 30 North and 30 South will be reduced to fix into the plane.
THE SIX MAPS
1) The First Map projection Image shows instead a Normal MERCATOR, which is the most widely used Conformal Projection. As it is possible to see in the image, this map preserves the Angles very well, but areas are inevitably deformed as well as distances do. Using more secant points (see paragraph above), could help to reduce this effects but it will never be possible to adjust the 3 properties of the projection (Conformity, Equal-Area, Equal-Distance). It is good for showing the whole world on a rectangular surface just to have an idea of all the continents it contains. The most wide use is done in Large Scale Topographic Maps and Nautical Charts, because on smaller areas such as less than one decimal degree, deformations are minimal. Ie. USGS Topographic Maps.
2) LAMBERT CONFORMAL CONIC Projection is widely used in Aeronautical Charts, and is made by intersecting a Cone on one Emisphere of the Ellipsoid or Sphere. The results is a map with two secant points corresponding to two parallels, where there is no distortion along the standard parallels, but distortion increases further from the chosen parallels. For a country like the US, all located into one Hemisphere and for most of its area close or between central arcs of latitude, it is a very useful and not much deforming projection.
3)The EQUIDISTANT CYLINDRICAL Projection preserves distances very good, but loses correctness of Areas and Angles. It is used when we want to make pretty accurate measurements, but we will not use it as a navigation map or to find out the surface extent of nations or regions.
4) The EQUIDISTANT CONIC is instead created by projecting all the two Hemispheres surfaces into a single Cone which starts from a single point, generally one of the Poles (North Pole usually). Areas are dramatically deformed in order to preserve distances. It is not very useful unless we are projecting only areas within 15-30 degrees from the center of the projection, the Pole.
5) The CYLINDRICAL EQUAL AREA is a projection widely used to represent all the surface of the globe. It maintains Areas Perfectly and Bearings pretty well, but dramatically exaggerates and stretch Continents and Items located far away from The Equator so Distances are inevitably and highly longer than the reality as far as we move north or south from the Equator.
It remains in every case a good projection for representing Countries' extensions and their are compared with the rest of the world.
6) USA CONTIGUOS ALBERS EQUAL AREA CONIC
The Sixth map is not used commonly, and we can explain why. Although Areas are preserved extremely well around all the surface represented, this projection results horrible for the preservation of both directions and Distances, which are reasonable only very close to the secant points of the Cone. The result is that only countries located close to the secant parallels are represented fairly well such as the United States in this case, which are also the center of the projection in order to be represented as much precisely as possible. It is definitely a Map I would use and center on a local region of the world, and I won't use for the representation of the whole globe.
PROBLEMS AND PERILS OF PROJECTION SYSTEMS
The most important Peril of projections is the fact that there are several standard ones but also everyone can create their own projection. This results in a big multitude of representations and maps that contain information not easily and immediately comparable. ARCGIS has a tool for changing the projection system of representations, but it could not contain the specific projection used to project the map and in this case we can lose important information contained such as distances or areas of the items, or, even worst, not realizing that we are using a wrong projection which is slightly different from the one the maps was created in. and we are then going to have incorrect data.
ADVANTAGES
In general, the enormous variability of projections allows us to use the best and close-to-reality representation system when we want to create or modify maps. Moreover, very useful tools such as ArcGis allowed us to easily manage projections, as long as we are competent and have the knowledge to use the right and proper projection at everytime.
the significance, perils and potential of map
projections based on this exercise. Be sure to clearly reference your six maps as
examples
Geographical Projections are used to reduce surfaces of spherical or other 3D shapes into a 2D models. Inevitably, some information is lost during this process, as it is not possible to represent a Sphere on a Plane. One important characteristic or projection process is that it can be adapted to different needs. In fact, there are basically infinite formulas we can use for making surfaces from Geometrical Shapes. It depends by the Intersecting point we use as a touching point from the hypothetical surface and the sphere (or ellipsoid), and which surface are we going to use to represent the plane. We can use for example a plane developed from a Cone or a Cylinder, or other shape with a curvature.
Personally, I think that one of the best projection is the Mercator secant in two points of the globe, because is able to also maintain areas better than a normal Mercator. This Projection uses a normal cylinder, but it has tangent 2 points at 30 degrees North and 30 Degrees South of the Equator with the Sphere. Areas North of 30 deg. North and South of 30 deg. South will be slightly bigger than the reality, while the arc between 30 North and 30 South will be reduced to fix into the plane.
THE SIX MAPS
1) The First Map projection Image shows instead a Normal MERCATOR, which is the most widely used Conformal Projection. As it is possible to see in the image, this map preserves the Angles very well, but areas are inevitably deformed as well as distances do. Using more secant points (see paragraph above), could help to reduce this effects but it will never be possible to adjust the 3 properties of the projection (Conformity, Equal-Area, Equal-Distance). It is good for showing the whole world on a rectangular surface just to have an idea of all the continents it contains. The most wide use is done in Large Scale Topographic Maps and Nautical Charts, because on smaller areas such as less than one decimal degree, deformations are minimal. Ie. USGS Topographic Maps.
2) LAMBERT CONFORMAL CONIC Projection is widely used in Aeronautical Charts, and is made by intersecting a Cone on one Emisphere of the Ellipsoid or Sphere. The results is a map with two secant points corresponding to two parallels, where there is no distortion along the standard parallels, but distortion increases further from the chosen parallels. For a country like the US, all located into one Hemisphere and for most of its area close or between central arcs of latitude, it is a very useful and not much deforming projection.
3)The EQUIDISTANT CYLINDRICAL Projection preserves distances very good, but loses correctness of Areas and Angles. It is used when we want to make pretty accurate measurements, but we will not use it as a navigation map or to find out the surface extent of nations or regions.
4) The EQUIDISTANT CONIC is instead created by projecting all the two Hemispheres surfaces into a single Cone which starts from a single point, generally one of the Poles (North Pole usually). Areas are dramatically deformed in order to preserve distances. It is not very useful unless we are projecting only areas within 15-30 degrees from the center of the projection, the Pole.
5) The CYLINDRICAL EQUAL AREA is a projection widely used to represent all the surface of the globe. It maintains Areas Perfectly and Bearings pretty well, but dramatically exaggerates and stretch Continents and Items located far away from The Equator so Distances are inevitably and highly longer than the reality as far as we move north or south from the Equator.
It remains in every case a good projection for representing Countries' extensions and their are compared with the rest of the world.
6) USA CONTIGUOS ALBERS EQUAL AREA CONIC
The Sixth map is not used commonly, and we can explain why. Although Areas are preserved extremely well around all the surface represented, this projection results horrible for the preservation of both directions and Distances, which are reasonable only very close to the secant points of the Cone. The result is that only countries located close to the secant parallels are represented fairly well such as the United States in this case, which are also the center of the projection in order to be represented as much precisely as possible. It is definitely a Map I would use and center on a local region of the world, and I won't use for the representation of the whole globe.
PROBLEMS AND PERILS OF PROJECTION SYSTEMS
The most important Peril of projections is the fact that there are several standard ones but also everyone can create their own projection. This results in a big multitude of representations and maps that contain information not easily and immediately comparable. ARCGIS has a tool for changing the projection system of representations, but it could not contain the specific projection used to project the map and in this case we can lose important information contained such as distances or areas of the items, or, even worst, not realizing that we are using a wrong projection which is slightly different from the one the maps was created in. and we are then going to have incorrect data.
ADVANTAGES
In general, the enormous variability of projections allows us to use the best and close-to-reality representation system when we want to create or modify maps. Moreover, very useful tools such as ArcGis allowed us to easily manage projections, as long as we are competent and have the knowledge to use the right and proper projection at everytime.
No comments:
Post a Comment